Recently, Wooldridge shared a working paper titled Two-Way Fixed Effects, the Two-Way Mundlak Regression, and Difference-in-Differences Estimators. He also shared a video, slides, and code to accompany to paper on his Twitter account.

The paper does a ton of stuff, and I will not attempt to go through or summarize it all. Instead, I will focus on just one part: the equivalence between an “extended” Two-Way Fixed Effects estimator and some recent alternative strategies for analyzing policy interventions in a Difference-in-Differences (DiD) framework.

As I noted in a previous post, there has been a lot of recent development in econometrics on the analysis of policy interventions using panel data. The “standard” approach for many analysts has been to use Two-Way Fixed Effects (TWFE). However, several authors have pointed out that in the presence of treatment effect heterogeneity – when treatment effect varies over time or by treatment “cohort” – TWFE can do weird stuff. In recent years, many papers have been written to explain exactly what quantities get estimated, and to propose alternative strategies (Goodman-Bacon 2021; Borusyak, Jaravel, and Spiess 2021; Callaway and Sant’Anna 2021; Strezhnev 2018; Liu, Wang, and Xu 2020).

In his paper, Wooldridge acknowledges that TWFE can produce weird results in such settings, but counters that

there is nothing inherently wrong with TWFE, which is an estimation method. The problem with how TWFE is implemented in DiD settings is that it is applied to a restrictive model.

He then goes on to describe a couple equivalent ways to make the model more flexible and account for heterogeneity, using Mundlak devices or an “extended” TWFE.

The extended TWFE approach is the one I focus on below. It can be very simple: Interact the treatment indicator with time and/or group-time dummies.

The rest of this notebook gives a “Proof by R” that TWFE with interactions can produce estimates of the Group-Time ATT which are very similar to those produced by the did software package by Callaway and Sant’Anna (2021).

Simulation

I begin by simulating data using a data generating process similar to (identical to?) “Simulation 6” from Baker, Larcker, and Wang (2021). The simulated data have a few interesting features:

1000 firms, located in 50 states, observed every year between 1980 to 2015.
Staggered treatment cohorts: Firms from states 1-17 are treated in 1989. Firms from states 18-34 are treated in 1998. Firms from states 35-50 are treated in 2015.
Treatment effects are heterogeneous across treatment cohorts: Effects are strongest in the 1989 cohort and smallest in the 2007 cohort.
Treatment effects are heterogeneous across time: Effects increase cumulatively from the year of treatment (see cumsum in the code below).

library("did")
library("broom")
library("fixest")
library("ggplot2")
library("data.table")

simulation6 = function() {
  dat = CJ(firm = 1:1000, year = 1980:2015)     [
    , time_fe := rnorm(1, sd = .5), by = "year"][
    , unit_fe := rnorm(1, sd = .5), by = "firm"][
    , state := sample(1:50, 1), by = "firm"    ]

  setkey(dat, state, firm, year)

  treatment_groups = data.table(
    state = c(1, 18, 35),
    cohort = c(1989, 1998, 2007),
    hat_gamma = c(.5, .3, .1))
  dat = treatment_groups[dat, roll = TRUE, on = "state"]

  dat                                                [
    , treat  := as.numeric(year >= cohort)          ][
    , gamma  := rnorm(.N, mean = hat_gamma, sd = .2)][
    , tau    := fifelse(treat == 1, gamma, 0)       ][
    , cumtau := cumsum(tau), by = "firm"            ][
    , error  := rnorm(.N, 0, .5)                    ][
    , y := unit_fe + time_fe + cumtau + error       ][
    , time_to_treat := year - cohort                ]

  return(dat)
}

dat = simulation6()

Estimation

With the dataset in hand, we use the fixest package to estimate a TWFE model in which the treatment indicator is interacted with both time-to-treatment dummies and cohort dummies:

etwfe = feols(y ~ treat : factor(time_to_treat) : factor(cohort) | firm + year, data = dat)

The variables 'treat:factor(time_to_treat)-27:factor(cohort)1989', 'treat:factor(time_to_treat)-26:factor(cohort)1989', 'treat:factor(time_to_treat)-25:factor(cohort)1989', 'treat:factor(time_to_treat)-24:factor(cohort)1989', 'treat:factor(time_to_treat)-23:factor(cohort)1989', 'treat:factor(time_to_treat)-22:factor(cohort)1989' and 111 others have been removed because of collinearity (see $collin.var).

# Clean the results
etwfe = as.data.table(tidy(etwfe))
etwfe = etwfe[
    , .(term = term, etwfe = estimate)][
    , group := as.numeric(gsub(".*cohort.", "", term))][
    , year := as.numeric(gsub(".*time_to_treat.(\\d+).*", "\\1", term)) + group][
    , .(group, year, etwfe)]

We use the did package to apply the Callaway and Sant’Anna (2021) strategy to estimate group-time ATT:

csa = att_gt(
    yname = "y",
    gname = "cohort",
    idname = "firm",
    tname = "year",
    control_group = "notyettreated",
    data = dat)

# Clean the results
csa = data.table(group = csa$group, year = csa$t, csa = csa$att)

Finally, we merge the results from those two strategies and plot group-time ATT estimates across time for two cohorts:

# merge the TWFE and CSA results
results = merge(etwfe, csa, by = c("group", "year"))
colnames(results) = c("Cohort", "Year", "TWFE w/ interactions", "CSA (2021)")
results[, Cohort := factor(Cohort)]

dat_plot = melt(results, id.vars = c("Cohort", "Year"))
ggplot(dat_plot, aes(Year, value, color = variable, linetype = Cohort)) +
  geom_line(size = 1.4) +
  theme_minimal() +
  labs(x = "Year", y = "ATT", color = "Estimator", linetype = "Cohort")

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.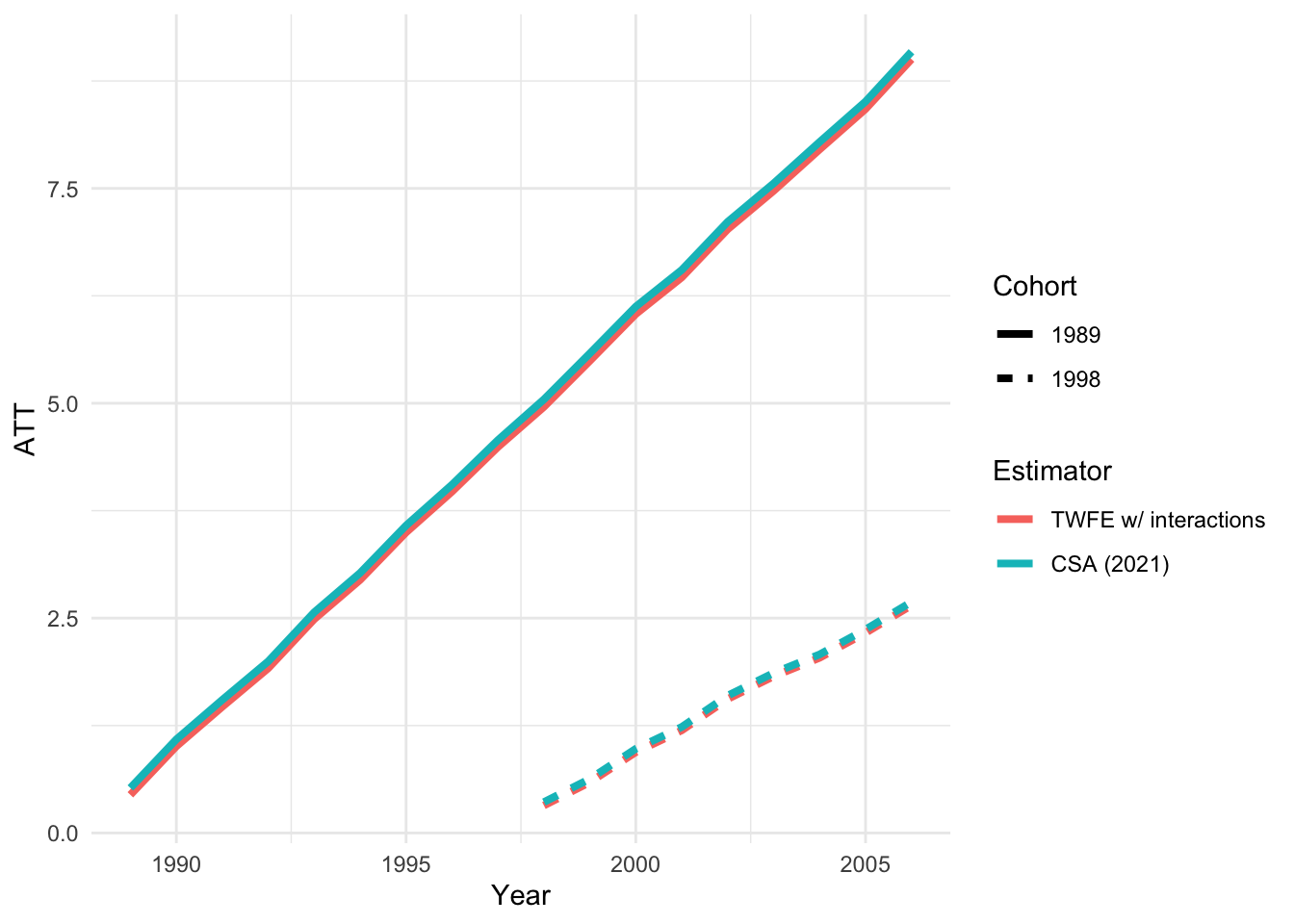

The estimates are so similar that lines are hard to distinguish visually. But we can see how close the two sets of results really are by plotting them against each other:

ggplot(results, aes(`TWFE w/ interactions`, `CSA (2021)`, color = Cohort)) +
  geom_point(size = 2) +
  geom_abline(intercept = 0, slope = 1) +
  labs(title = "On the 45 degree line, estimates of the group-time ATT\nare identical under the two strategies.") +
  theme_minimal()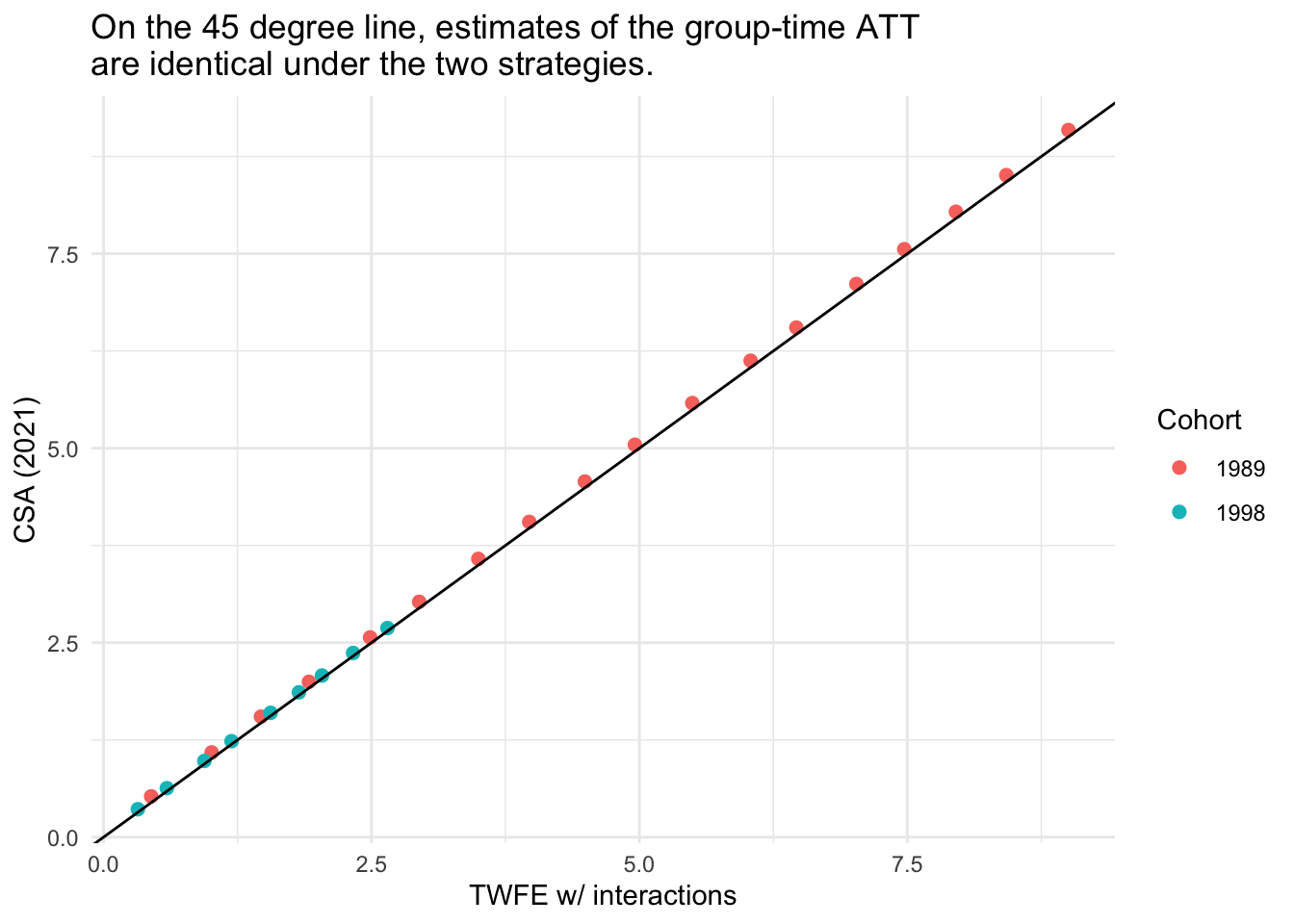

That’s all I have to show you today. To reiterate, there is a bunch more stuff in the Wooldridge paper and, frankly, I haven’t digested all of it yet. Make sure you click on the links above to learn more, and get in touch with if you want to share your different interpretation, or if you feel like different points should have been emphasized.

More on the Baker simulation

Simulated data

Adapted from Baker via Chabé-Ferret:

/https://chabefer.github.io/STCI/NE.html#difference-in-differences-with-instrumental-variables

library(fixest)
library(broom)
library(tidyverse)
library(ggokabeito)
theme_set(theme_minimal())
scale_colour_discrete <- scale_colour_okabe_ito
scale_fill_discrete <- scale_fill_okabe_ito

# set seed
set.seed(20200403)
# Fixed Effects ------------------------------------------------
# unit fixed effects
unit <- tibble(
unit = 1:1000, 
unit_fe = rnorm(1000, 0, 1),
# generate state
state = sample(1:40, 1000, replace = TRUE),
# generate treatment effect
mu = rnorm(1000, 0.3, 0.2))

# year fixed effects 
year <- tibble(
year = 1980:2010,
year_fe = rnorm(31, 0, 1))

# Trend Break -------------------------------------------------------------
# Put the states into treatment groups
treat_taus <- tibble(
  # sample the states randomly
  state = sample(1:40, 40, replace = FALSE),
  # place the randomly sampled states into five treatment groups G_g
  cohort_year = sort(rep(c(1982, 1991, 1998, 2004), 10)))

# make main dataset
# full interaction of unit X year 
dat <- expand_grid(unit = 1:1000, year = 1980:2010) %>% 
  left_join(., unit, by = "unit") %>% 
  left_join(., year, by = "year") %>% 
  left_join(., treat_taus, by = "state") %>% 
  # make error term and get treatment indicators and treatment effects
  mutate(error = rnorm(31000, 0, 0.5),
         treat = ifelse(year >= cohort_year, 1, 0),
         tau = ifelse(treat == 1, mu, 0)) %>% 
  # calculate cumulative treatment effects
  group_by(unit) %>% 
  mutate(tau_cum = cumsum(tau)) %>% 
  ungroup() %>% 
  # calculate the dep variable
  mutate(dep_var = unit_fe + year_fe + tau_cum + error,
         w = as.numeric(year >= cohort_year))

Model

Adapted from Wooldridge (2021)

mod <- feols(dep_var ~
             w : i(cohort_year, i.year) +
             i(year) |
             unit,
             data = dat)

Results

cohorts <- c(as.character(sort(unique(dat$cohort_year))), NA)

res <- mod %>%
    # extract
    tidy(conf.int = TRUE) %>%
    # ignore year dummies
    filter(grepl("^w", term)) %>%
    # cleanup
    separate(term, sep = "::", into = c(NA, "cohort", "year")) %>%
    mutate(cohort = gsub(":.*", "", cohort),
           year = as.numeric(year),
           time_to_treatment = year - as.numeric(cohort)) %>%
    # ATTs are available for a cohort only until the next cohort gets treated
    mutate(cohort_next = as.numeric(cohorts[match(cohort, cohorts) + 1])) %>%
    filter(year < cohort_next)

ggplot(res, aes(x = time_to_treatment,
                y = estimate,
                ymin = conf.low,
                ymax = conf.high,
                color = cohort)) +
    # Baker simulation:
    # tau is a random variable equal with mean 0.3
    # cumsum(tau) = ATT
    geom_abline(intercept = .3, slope = .3) +
    geom_pointrange() +
    labs(x = "Time to treatment",
         y = "ATT",
         color = "Cohort",
         title = "Group-Time ATTs estimated using TWFE & Interactions.",
         subtitle = "The black line shows the truth.")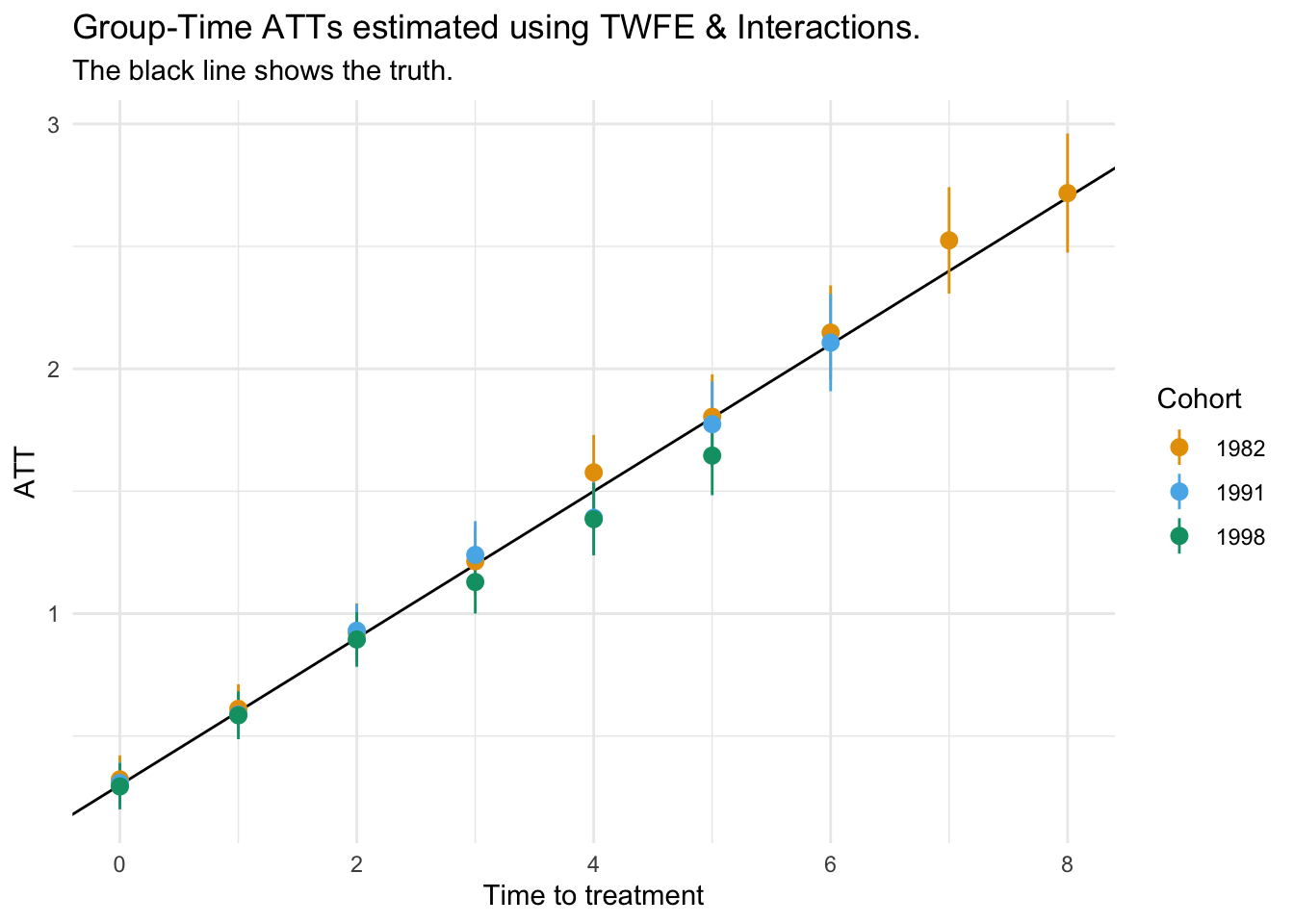

Notes:

The ATTs for the final cohort (2004) are not identified.
We only get Group-Time ATTs for group j for the years before the next cohort gets treated. This explains why there are more estimates for certain cohorts in the Figure above.

References

Baker, Andrew, David F Larcker, and Charles CY Wang. 2021. “How Much Should We Trust Staggered Difference-in-Differences Estimates?” Available at SSRN 3794018. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3794018.

Borusyak, Kirill, Xavier Jaravel, and Jann Spiess. 2021. “Revisiting Event Study Designs: Robust and Efficient Estimation.” arXiv Preprint arXiv:2108.12419.

Callaway, Brantly, and Pedro H. C. Sant’Anna. 2021. “Difference-in-Differences with Multiple Time Periods.” Journal of Econometrics, December. https://doi.org/10.1016/j.jeconom.2020.12.001.

Goodman-Bacon, Andrew. 2021. “Difference-in-Differences with Variation in Treatment Timing.” Journal of Econometrics.

Liu, Licheng, Ye Wang, and Yiqing Xu. 2020. “A Practical Guide to Counterfactual Estimators for Causal Inference with Time-Series Cross-Sectional Data.” SSRN Electronic Journal. https://doi.org/10.2139/ssrn.3555463.

Strezhnev, Anton. 2018. “Semiparametric Weighting Estimators for Multi-Period Differencein-Differences Designs.” In Annual Conference of the American Political Science Association, August. Vol. 30.